When a probabilist embarks in the quest of exploring the natural selection
notably through the conditioning of probability distributions
keywords : quasi-stationary distribution (QSD), survival capacity, Q-process, Large deviation, adaptation, selection, variation
Publications
preprint : https://arxiv.org/abs/1802.02409
Unique Quasi-Stationary Distribution, with a possibly stabilizing extinction
We establish sufficient conditions for exponential convergence to a unique quasi-stationary distribution in the total variation norm. These conditions also ensure the existence and exponential ergodicity of the Q-process, the process conditioned upon never being absorbed. The technique relies on a coupling procedure that is related to Harris recurrence (for Markov Chains). It applies to general continuous-time and continuous-space Markov processes. The main novelty is that we modulate each coupling step depending both on a final horizon of time (for survival) and on the initial distribution. By this way, we could notably include in the convergence a dependency on the initial condition. As an illustration, we consider a continuous-time birth-death process with catastrophes and a diffusion process describing a (localized) population adapting to its environment.
preprint : https://arxiv.org/abs/1902.01441
Exponential quasi-ergodicity
for processes with discontinuous trajectories
This paper tackles the issue of comparing asymptotically the survival of a Markov process with extinction, depending on its initial condition. Such a comparison is a crucial step in recent techniques for proving exponential convergence to a quasi-stationary distribution. We introduce a weak form of the Harnack inequality as the essential ingredient for such a comparison. This property is actually a consequence of the property of convergence we intend to prove. Although its flexibility makes it difficult to grasp its full potential, we show in our illustrations how simply and efficiently it can be used. This makes it possible to treat such an exponential convergence for new classes of càdlàg strong Markov processes. As illustrations, we consider two continuous-time processes on Rd that do not satisfy the classical Harnack inequalities, even in a local version. The first one is a piecewise deterministic process while the second is a pure jump process with restrictions on the directions of its jumps. Although newly introduced, these examples are yet among the simplest ones for which our techniques are fruitful.
preprint : https://arxiv.org/abs/1903.10165
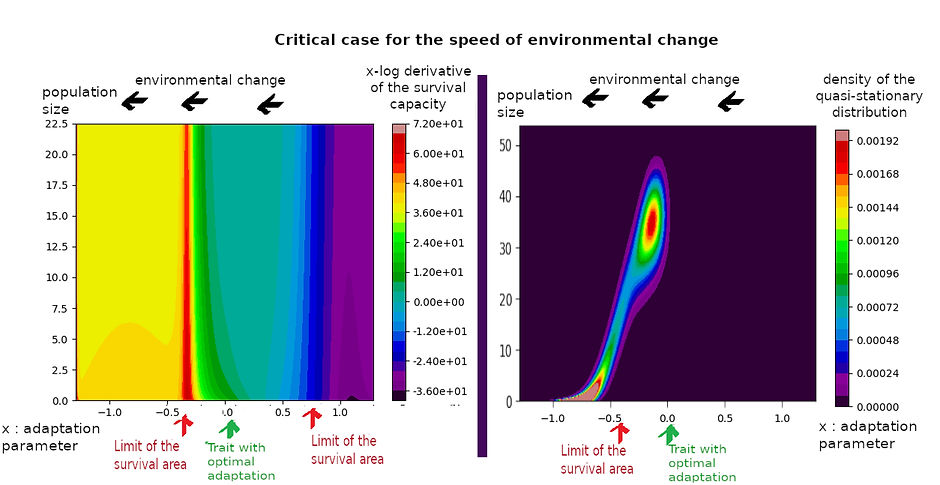
Adaptation of a population to a changing environment under the light of quasi-stationarity
We analyze the long-term stability of a stochastic model designed to illustrate the adaptation of a population to variation in its environment. A piecewise-deterministic process modeling adaptation is coupled to a Feller logistic diffusion modeling population size. As the individual features in the population become further away from the optimal ones, the growth rate declines, making population extinction more likely. Assuming that the environment changes deterministically and steadily in a constant direction, we obtain the existence and uniqueness of the quasi-stationary distribution, the associated survival capacity and the Q-process. Our approach also provides several exponential convergence results (in total variation for the measures). From this synthetic information, we can characterize the efficiency of internal adaptation (i.e. population turnover from mutant invasions). When the latter is lacking, there is still stability, but because of the high level of population extinction. Therefore, such a characterization must be based on specific features of this quasi-ergodic regime.
preprint : https://arxiv.org/abs/1903.10161
Two level natural selection with a quasi-stationarity approach
In a view for a simple model where natural selection at the individual level is confronted to selection effects at the group level, we consider some individual-based models of some large population subdivided in a large number of groups. We then obtain the convergence to the law of a stochastic process with some Feynman-Kac penalization. To analyze the limiting behavior of this law, we use a recent approach, designed for the convergence to quasistationary distributions, that generalizes the principles of Harris recurrence. We are able to deal with the fixation of the stochastic process and relate the convergence to equilibrium to the one where fixation implies extinction. We notably establish different regimes of convergence. Besides the case of an exponential rate (the rate being uniform over the initial condition), critical regimes with convergence in 1/t are also to notice. We finally address the relevance of such limiting behaviors to predict the long-time behavior of the individual-based model.
ESAIM: PROCEEDINGS AND SURVEYS, 2020,
Vol. 68, p. 123-152
Individual-based models under various time-scales
Les résultats récents présentés dans cet article décrivent des limites d’échelles de modèles individus-centrés. Grâce à eux, nous allons mettre en lumière les différentes échelles de temps car- actéristiques des variations démographiques et de la sélection naturelle. L’objectif n’est pas d’être exhaustif, tant au niveau mathématique que biologique. Néanmoins, ces résultats sont très complé- mentaires les uns des autres. Ils fournissent un aperçu des principales échelles de temps d’intérêt. Ils englobent notamment l’échelle de temps de la vie d’un individu, celle plus longue où la population peut être décrite comme une entité avec ses caractéristiques propres qui dirigent les dynamiques dé- mographiques, et au moins quatre autres échelles imbriquées sur lesquelles la sélection joue un rôle. La dynamique limite est généralement déterministe. Pour autant, puisque l’action de la sélection se base sur l’aléa présent dans l’histoire des individus, les probabilités apparaissent comme un élément clé pour comprendre ces résultats. Par ailleurs, la stochasticité peut aussi être conservée à la limite, par exemple pour modéliser de rares événements de fixation de mutations.
joint work in progress with M. Mariani and E. Pardoux
https://arxiv.org/abs/2007.14715
Quasi-stationarity in the Müller's ratchet model
Müller's ratchet model enables to analyse the adaptation stability of a population when deleterious mutations regularly affects new individuals. Here, we condition on the fact that the fittest individuals are still present in the population. Our purpose is to ensure the exponential quasi-ergodicity of the processes (with or without an upper-bound on the number of accumulating deleterious mutations). We also expect to ensure that individuals with too many deleterious mutations play a negligible role both for the survival of the fittest subpopulation and for the quasi-ergodicity of the population on a whole.
project with the support of D. Kim
Large deviation in the history of suviving processes
We give a general scheme to ensure the conditions of Gärtner-Ellis Theorem for evaluations of the empirical measure. We show that up-to-date conditions for ensuring the convergence to a quasi-stationary distribution can be applied efficiently. By this mean, we are able to prove Large Deviation results even with a conditioning that the process is not extinct at the end of the evaluation. The domain on which these Large Deviation results apply is implicitly given by the range of penalization for which one can prove the above-mentioned results of quasi-stationarity. We propose a way to relate the range of controlled deviations to the range of admissible penalization. Central Limit Theorems are deduced from these results of Large Deviations. As an application, we consider the empirical measure of position and jumps of a continuous-time process on an bounded domain of Rd. This model is inspired by the adaptation of a population to a changing environment. Jumps makes it possible for the process to face a deterministic dynamics leading to high extinction areas.
joint work in progress with Viktor Bezborodov, Tyll Krüger and Cornelia Pokalyuk
Infection dynamics between cities under a lockdown policy
The goal of our project is to compare the efficiency of different local lockdown policies when an infection spreads between cities (or more general regions). We model the infection dynamics on a random network where each node represents a city. We take the size of a city as a parameter for its connectivity to other cities. Because of its empirical relevance, we are particularly interested in city size distributions that are heavy-tailed. Once a city gets infected it is set under lockdown according to one of the following two lockdown policies, depending on a certain number of infected citizen. In variant $(U)$ this number of citizens takes the same value $N$ for any city, while in variant $(P)$ it corresponds to a certain proportion $p$ of the citizens. We define and determine a basic reproduction number R_0 that represents the strength of the epidemic initially. We find that R_0 of variant $(U)$ usually lower-bounds the corresponding R_0 of variant $(P)$ (at least this is proved if the influx and efflux are not biased against large cities). Moreover, we investigate (mainly by means of simulations and motivated by empirical data) to which extent R_0 can be relevant to capture the initial phase of disease propagation between the cities.
Teaching
Conferences and workshops
avril 2017
Modelling Biological Evolution 2017 :
http://www.math.le.ac.uk/people/ag153/homepage/MBE_2017/MBE_2017_1.htm
Contact
Institut für Mathematik,
Goethe Universität Frankfurt
aurelien.velleret_at_nsup_dot_org



